by Bethanie Edwards
Hi, a mercury atom here. I’m currently floating in a water bottle of a delegate at the INC5 mercury negotiations in Geneva. As you know, the global community is coming together this week to negotiate ways to prevent my release into the environment. How exactly do I and my fellow mercury atoms make it into the environment to begin with? Let me share my experience with you.
For much of my life I was just a mercury atom sharing electrons with my best friend, a sulfur atom, deep in the earth as cinnabar. My potential toxicity was masked by my rosy appearance. I was expecting to spend my entire life nestled away in the Earth’s crust. But suddenly, I was startled, a loud persistent thud getting closer and closer. It was 1500 AD, and Spanish miners had just dug me out of my lithospheric home in the mountain-sides of Almaden, Spain. That’s when I began my journey, contributing to the 350,000 metric tons of mercury that humans have released into the environment over the last 4000 years.

Illustration from Erker (1574)
After traveling to a monastery, monks began heating me up. I could feel my bond with sulfur dissipating; I was entering the vapor phase. I was collected in a distillation bulb as I evaporated, separated from the cinnabar. Little did I know, I’d soon be forced into a new partnership (albeit a brief one).
Once condensed into my liquid state and mixed with sluice from gold panning, my affinity for binding with other metals led me to bind together with all of the gold in the river bed sluice, separating the gold from the rock. When the rock was discarded the monks begin heating me up again, ending my short amalgamation with gold. However, this time as I vaporized, I escaped into the atmosphere.
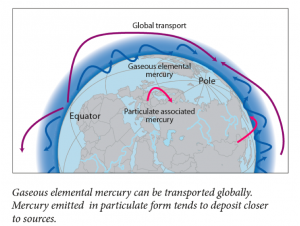
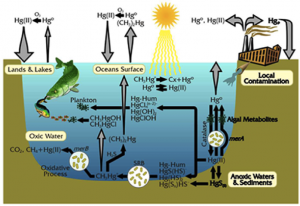
The vapor pressure of mercury is very high, so I floated all the way into the upper troposphere and caught a wind current to the North Pole. Along the way I met a few other mercury atoms. Most of them had found their way into the atmosphere after weathering into rivers and then evaporating, or after being emitted from the eruption of a volcano. I bummed around in the Arctic troposphere for about 6 months. As I recall, there were quite a few bromine atoms around. I ran into one, lost a few electrons, and then stuck to it. Then we began falling through the atmosphere, luckily there was snow to break our fall. There I waited until summer, when the snow began to melt and I was washed into a fjord.
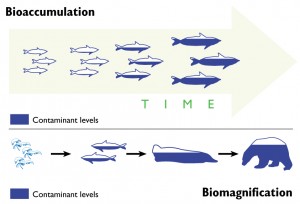
As the summer progressed in the fjord, phytoplankton bloomed and then died. The bacterial populations began to grow exponentially and, before I knew it, the bacteria had used up all the oxygen. When bacteria deplete all the oxygen gas in an environment, they move on to using other molecules to make a living. Once they started using sulfate (SO42-), my old friend sulfur re-entered the picture. I bound with it and, not too long afterward, one of those bacteria sucked me into her cell. I’m not sure if the bacterium was just interested in the sulfur that I was attached to, or if she found me to be too toxic, but—to my horror—the bacterium quickly tore away the sulfur and stuck me with a methyl group.
Now, I’m not trying to be prejudiced against carbon, but it’s really not a good influence on me. I have enough toxicity problems on my own. And when I’m bound to an organic carbon, I can’t resist diffusing into organisms, be it fish, shellfish, or humans. That is exactly what happened. After the water that I was residing in was re-oxygenated, a fish came along and I entered its body through the gill tissue, and as I was a methylmercury molecule by then, I wasn’t the only one to do so.
Eventually my fishy friend’s luck ran out; a fisherman caught him and cooked him up for dinner. I stayed inside the fisherman until he lived out his days and was cremated, and I was released back into the atmosphere.
I felt bad for the poor fellow but I was perfectly happy to be back in the atmosphere. I was looking forward to seeing the Arctic again. But to my surprise, I started falling to the Earth very shortly after being emitted. It must have been all the soot that I was associated with. I was deposited on the forest floor. As the seasons turned and leaves fell and decayed, I became buried in the soil. The rains came and went, but I stayed in the forest getting buried millimeter by millimeter deeper into the soil with each passing year. Until the day the fires came, that is.
Sometimes forest fires burn so hot that they scorch the soil. When this occurs, volatile elements like me can be vaporized and released into the atmosphere. While I will admit I was sequestered in the soil for quite a while, I did not expect to see so many other mercury atoms when I returned to the atmosphere. I met mercury atoms that had found their way to the atmosphere after being in fillings in people’s mouths, atoms that used to reside in light bulbs, several atoms that were used recently in gold mining in the depths of the jungle, and of course the atoms that were released from coal.
This time when I met and bound with a bromine radical, I was in the atmosphere over the Swiss Alps. Since Switzerland is a temperate region, it took much longer to get deposited than it had when I was in the Arctic. However, I eventually landed in the waters of the Alps and ultimately made it into the water bottle of an INC5 delegate.
Since I am one of 1.5×1015 mercury molecules in this water bottle alone, I sure do hope that they agree upon and sign a treaty with teeth!